强化学习的生物学基础

斯金纳的操作性条件反射

总结起来，从生物学基础来看，强化理论是通过给予奖励和惩罚、来改变智能体的行为方式。

智能体表现好、就通过某些方式给奖励；表现不好，就给予惩罚。

（随机奖励指的是 不确定何时会获得奖励的机制。研究表明，这种不确定性会使智能体更投入于某种行为，因为它们总是期待下一次可能的奖励。）

强化学习建模

状态模型

• 初始状态 $S_0$
• 当前玩家 $C$
• 动作集合 $A$
• 状态转移 $P$
  • $P(S_{t+1}|S_t,A_t)$表示在时间 t, Agent 在状态$S_t$下采取动作$A_t$ 后转到下一个状态$S_{t+1}$的概率。
  • 如何衡量一个环境的复杂程度呢？环境可能达到的所有状态、我们称为状态空间。智能体可能执行的所有动作，称为动作空间。如果这两个空间越大，那么环境就越复杂
• 终止状态 $S_T$
• 奖励 ： 某个状态下，智能体采取某动作后得到的分数。

智能体（问题的解）模型

那智能体优化的目标是什么呢？什么叫做聪明呢？

寻找一个最优策略，就是要最大化，从初始状态$S_0$到终止状态$S_T$上、每一步收益 R 的累积。

强化学习就是要得到一个好的策略 π ，使之可以得到好的收益。

策略 $\pi$

• $A_t \leftarrow \pi(S_i)$ 用以表示智能体的策略，也即在每一个状态 $S_t$下选择动作 $A_t$的规则或函数。
• 策略 π 是状态 S 到动作 A 的映射关系，给出了智能体在状态 S 下如何选择动作 A 的决策方法。
• 注意：策略 π 是 全局性 的，任何状态下都要能够给出动作选择。
• 确定性策略 π：对于每个状态 $s \in S$，策略 $\pi(S)$ 总是返回一个确定的动作$A$

目标

寻找最优策略使得收益最大

例子：井字棋的建模

与先前学习的假设对弈双方都是最聪明（双方都采用最优策略）的 MINIMAX 算法不同，强化学习仅仅假设：

1. 敌人采用的是 确定性策略 （给定 S 下有确定的 A，而不是随机的 A），但是不一定是最优策略。
2. 我们可以和敌人进行 多次对弈

基本思想：从而学习到一个好的对敌策略。

显然，这样的假设更为真实，因为我们能够利用真实情况中，敌人决策的失误来对应的调整我们的策略。

问题建模

初始状态：空棋盘

当前玩家：下子的一方

动作：落子到空的位置

状态转移：落子后棋盘的状态

终止状态：棋盘满或者一方获胜

奖励：胜利+1，失败-1，平 0

解与目标

策略$\pi$:

使用 状态估值表，每个状态一个入口（表项），记录从该状态出发到终局的胜率。根据状态估值表选择动作。

• 学习策略$\pi_1$：大概率选择估值最高的下一个状态，小概率随机选一个动作（探索）
• 目标策略 $\pi_2$：每次选择通往估值最高的下一个状态（贪心）的动作，也即表示在每个状态下选择最优动作的规则。

目标（问题的解）：

最优策略 $\pi^*$：使得智能体从初始状态$S_0$ 下到最终的效率 / 胜率最大

训练过程

1. 建立状态估值表 $3^9$的最多状态，直接存

   估值表函数初值：（根据游戏规则）

   • 三个 X 连成一线的状态，价值为 1，因为我们已经贏了。
   • 三个 O 连成一线的状态，价值为 0，因为我们已经输了。
   • 其他状态的值都为 0.5，表示有 50% 的概率能贏。

2. 多次玩 目的：让估值表更加准确

   1. 利用：大概率贪心选价值最大的地方下
   2. 探索：偶尔随机地选择以便探索之前没有探索过的地方

   利用和探索要平衡

3. 边下边修改状态的值, 使得它更接近真实的胜率。

   $$ V(S_t) \leftarrow V(S_t) + \alpha[V(S_{t+1})-V(S_t)] $$

   其中 $\alpha$是一个小的正的分数，称为步长参数，或者学习率

   • 初值 $S_0$：只有终局的价值是正确的，中间局面的价值都是估计值 0.5（而这是错的）
   • 过程中：状态价值从后面向前传导
   • 分析：假设我们一直在一条路径上反复走，每走到终点一次，终局价值至少向上传一步，走多了终将把这个终局的输赢带到最上面的初始节点，于是我们在初始节点就会知道最后的输赢

小结

• 将对手建模在环境里；每次采取动作后面临的状态都是对手执行完它的动作后的新状态；（也可以建模成多智能体博弈问题，有一个对手决策模型，轮到对手落子时让对手模型决策）
• 用值函数表存储状态估值/值函数表 V(S)
• 通过不断对弈更新值函数表
• 根据值函数表、可以得到贪心选最优动作 π*

问题模型的泛化和分析

将概率加进来

环境 && 智能体

模型

• 初始状态 $S_0$(state)

• 当前玩家 C（current player(s)）

• 动作 A(action)

• 状态转移 P(transition)

• 终止状态 ST(terminate state)

• 奖励 R(reward)

• 策略 π

• 目标（问题的解）

• 最大化期望累积收益 G

环境：状态转移模型 P 和奖励 R

那么，我们让这个模型能表达更宽泛的问题，我们就要把概率加入这个模型。就是我做一个动作之后，我下一时刻的状态不是确定性的。而是有概率的。

• 状态不一定是确定性的，可以按照概率转移
• 奖励也不一定是确定性的，可以一个概率奖励

智能体：策略 π 和累积收益 G

• 策略 π 给出的动作选择可以是确定的，也可以是一个概率分布
• 折扣因子 γ ：（ 0 ≤ γ ≤ 1 ），描述未来收益的重要程度
  • 若为 1，则近的收益和远的收益一样重要
  • 若为 0，则只看下一步的收益（最贪心）
• 累积收益$G = R1+γR_2+γ^2R_3+…=∑{i=1}^Tγ^{i−1}R_i $

奖励函数对智能体最优策略的影响

• 奖励力度对智能体策略影响

策略的评估和最优策略

策略 π 的好坏用 状态价值$V_π$ 来评估：

• 状态价值$V_π$（S） 表示从 S 出发执行策略 π 能获得的累积收益；
• 结束状态（如果有）的价值，总是零

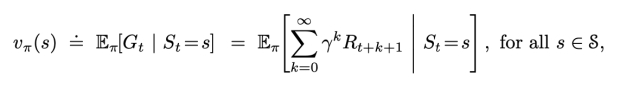
状态价值$V_{\pi}$和动作价值$Q_{\pi}$

• 动作价值$V_\pi(s， \alpha)$ ： 表示从 s 出发并做出动作 $\alpha$ ，之后执行策略 $\pi$ 能够获得的累计收益

  

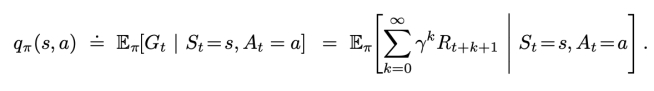
V,Q 关系：

强化学习的任务

智能体寻找最优策略的路径

智能体使用策略 π0（开始可能是随机的）与环境交互，产生经验（Experience

• s01,a01,r11,s11,a11,r21,s21,a21,r31,s31,a31,……. 计算 G1 以更新 π0

• π0s02,a02,r12,s12,a12,r22,s22,a22,r32,s32,a32,……. 计算 G2 以更新 π0

• π0s03,a03,r13,s13,a13,r23,s23,a23,r33,s33,a33,……. 计算 G3 以更新 π0

  智能体根据经验改进 π0 得到 π1，再用 π1 与环境交互以期获得更大

• Gs01,a01,r11,s11,a11,r21,s21,a21,r31,s31,a31,……. 计算 G1 以更

• π1s02,a02,r12,s12,a12,r22,s22,a22,r32,s32,a32,……. 计算 G2 以更

• π1s03,a03,r13,s13,a13,r23,s23,a23,r33,s33,a33,……. 计算 G3 以更新 π1……

如此往复，直到得到最（更）好的 π 前面看到的打砖块 AI 和王者鲁班七号 AI 都是这么得来

多臂老虎机问题

一个单臂老虎机，就是你给它投个币，相当于你摇它一下，它会给你吐出个随机的收益，这么一个赌博机器。这个收益服从正态分布。

但是多臂老虎机，指的是有一排老虎机摆在你面前，一个人占一排。不同机器的收益是不一样的，服从分布的均值和方差你是不知道的。


• 没摇过的有个缺省值，例如：0
• 时间 t 时选的动作为 At, 对应的奖励为 Rt. 动
• 作 a 的价值为 Q*(a)≈ E [ Rt | At = a ] . （老虎机问题中，状态 s 是不变的，不考虑 s 了）
• 

计算动作价值 q(s,a)

计算动作价值的一般形式。

新的估计 = 老的估值 + 当前步数 X 误差。

代码的话，刚开始 Q 和 N 都为 0 循环的时候，有个 epsilon 是一个很小的值。大概率根据 Q 最大的来选择动作 A。但有小概率随机选择动作，达到探索的功能。

然后后面就是更新 Q 了

大数定理，无限次后, Qt(a) 收敛至 Q*(a)

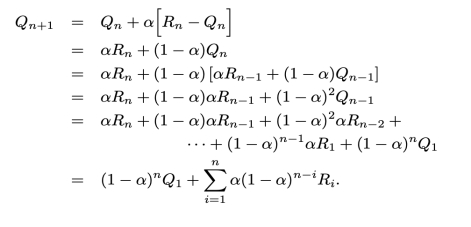
取 α = 1/nα 随时间变小 Qn 趋近于均值

贪心 v.s. $\epsilon $ 贪心

贪心核心思想：大部分时间选择贪心动作，偶尔随机选择。

$\epsilon $ 通过引入 随机性 来鼓励探索，避免陷入局部最优。

2000 次多臂老虎机

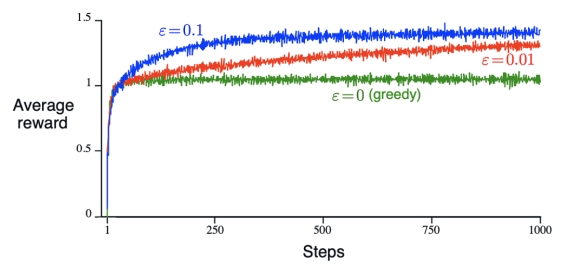
$\epsilon 贪心$ v.s. 乐观初始值贪心

乐观初始值贪心

• 负面：参数设定依赖：初值需要由人工给出，且设定不当可能影响算法性能。
• 正面：提供先验知识：合理的初值能提供先验经验，帮助算法确定奖励的期望量级。
• 学习效率：初值越准确，算法需要的调整次数越少，学习效率越高。

对比 Q1(a) = +5（探索鼓励） 和 Q1(a) = 0

• 如同人生，期望高就会勇于尝试新路径！但找到方向的时候，别乱探索了！
• 乐观初值鼓励探索，对于固定问题是非常有效的小技巧，但是并非是普遍有效的鼓励探索的方法
• 所以，如果情况变了，你还是要探索的！例如，对于非固定问题不管用，因为它鼓励探索是临时性的，为什么？并非主动探索，旁边有人变好它是不觉知的，遭遇大挫折时才会改变

乐观初始值贪心适用性：

• 固定问题：问题环境和奖励机制在整个学习过程中不发生变化，也即 P(s′∣s,a)P(s′∣s,a) 和 R(s,a)R(s,a) 固定，乐观初值有效

  利用 高初值 鼓励探索，迅速收敛到最优解。

• 非固定问题：问题环境或奖励机制会随时间变化，也即 P(s′∣s,a,t)P(s′∣s,a,t) 和 R(s,a,t)R(s,a,t) 随时间 tt 变化，乐观初值探索 不适用，ϵϵ 贪心更适用。

  通过 随机选择 保持探索，适应环境变化。

UCB（upper-confidence-bound）

实蒙特卡洛搜索的方法，是从这里进化来的。

Argmax 选动作的时候，又要看估值、又要看新鲜程度。这个想法在蒙特卡洛树搜索的时候用过。 UCB 将 “当前估值” 和 “新鲜程度” 加权和。

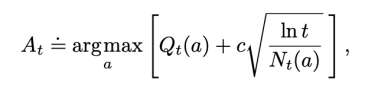
Gradient Bandit Algorithm

核心思想：

• ϵ 贪心大概率选最好的动作，其他动作 等同对待，其实也可以给每个动作一个对应的选择概率
• 通过给每个动作 a 一个 数值优先度 $H_t \in \mathbf{R}$来影响选择概率。
• 优先度越大，动作被选中的概率越大。

据此，我们给出如下设计：

• 采用 Softmax 函数归一化，使所有可行动作的概率和为 1

• 初始时，所有动作的倾向性相同（$H_1$ = 0）

• 在每一步，按概率选择了动作 $A_t$ 后得到及时奖励 $R_t$，根据奖励 $R_t$ 的大小，修改所有动作的优先度

  合理的划分出好的动作和坏的动作

  

总结

• $\epsilon$贪心算法有一小部分时间随机选：固定概率的随机探索
• UCB 偏向尝试次数小的动作：根据统计的探索、更聪明的探索
• 梯度下降法不是估计动作的价值，而是动作的优先顺序，使用 softmax 选动作. 其实有探索，因为动作采用 softmax 有概率
• 简单的设置乐观初值可以使得贪心算法也具有相当的探索性