问题描述模型

一个问题的定义

1. 初始状态 $S_0$。
2. 可选动作。在一个给定状态 s, ACTIONS(s) 返回一组可能的动作。
3. 状态转移模型。在状态 s 下执行动作 a 之后所到达的状态用 RESULT(s,a) 表示。 一个状态经过一个动作后来到的下一个状态我们称之为后继状态 。 初始状态、动作、状态转移模型构成了状态空间。 状态空间构成一幅有向图。 路径是从一个状态出发通过一系列动作所经过的状态序列。
4. 目标状态。
5. 路径花费。每条路径可以有一个花费，用来度量解的好坏。

一个问题的解 是从初始状态出发到达目标状态的一个动作序列。解的质量可以用路径的花费来度量。 最优解是所有解中花费最小的一个。

eg: 罗马尼亚寻径问题

1. 初始状态：In（Arad）
2. 可行动作：在 Arad，可选的动作是三个，分别去到 Z，S，T 三市
3. 状态转移，走了一条路之后到了哪里呢？例如说走了去 Z 市的路，后继状态就是 In（Z）。这里所有城市构成状态空间，所有道路构成动作空间。路径就是从一个城市到另一个城市的通路。
4. 目标状态：因为最终要去 Bucharest，所以到了 Bucharest，就不用再往下走了。
5. 路径花费，就是把从 Arad 走到 Bucharest，的路径上的每段路的长度加起来

e g: 八数码问题

状态: 一个状态描述了八个数字和一个空格所在的位置。

1. 初始状态: 任何一个状态都可以是初始状态。
2. 动作: 空格可以上、下、左、右移动。只要移动后还在 3*3 的方格内。
3. 状态转移模型: 给定一个状态和动作，给出之后的状态。
4. 目标: 给出想要达到的数字和空格分布状态
5. 路径花费: 每步花费 1, 路径花费就是移动的总步数。

搜索求解

搜索树

父节点，子节点，开节点，闭节点，搜索策略

一个状态经过一个动作，到了另一个状态。那么我们称发生动作之前的状态是父节点，而动作发生后的后继状态，称为子节点。

如果一个状态，没有节点，也就是说不能再往下搜索了，那么这个状态称为叶节点。没有儿子可展开的点叫叶节点。

开节点和闭节点

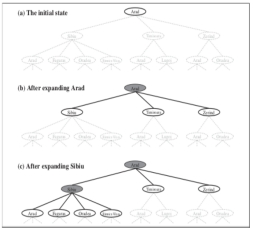
1. 最开始，树上只有根节点，也就是初始状态。搜索是一个动态过程。整个搜索的过程就是不断依据可行动作展开搜索树的过程。
2. 然后展开一步以后，我们多了几个新的叶节点，也就是对于根节点的子节点，这几个节点称为开节点，因为是刚刚展开的。英文叫做 frontier 也叫 open list。
3. 再展开一步以后，我们看多了几个新的叶节点，这些新的叶节点和原来的叶节点一起，都是叶节点。这个时候，闭节点是什么呢？图中灰色的节点称为闭节点，因为他们是已经被展开过的了。英文叫做 closed list 或者 explored set，explored 的意思是已经被探索过的节点。

搜索策略 对于一个算法而言，我们在一个时刻有那么多的开节点，先展开谁、后展开谁，就构成了不同的搜索策略搜索策略

就是如何在开节点集上，选择一个节点，把它优先展开。在最开始，树上只有根节点，也就是初始状态。事实上，搜索是一个动态过程。整个搜索的过程就是不断依据可行动作展开搜索树的过程。展开搜索树我们要做的就是先展开谁，后展开谁。如何选择下一个节点去展开被称为 search strategy 搜索策略。

树搜索，图搜索

树搜索：

我们看看这个 Tree-Search 的函数，输入的是一个问题 problem，就是我们刚刚定义的问题五元组。函数返回 return 的是一个解决方案 solution，或者告诉我们找不到解 failure。

最开始初始化 frontier，frontier 就是一个开节点，最开始把开节点设置为问题的初始状态，问题开始于一个点。然后，我们做一个循环，首先看看 frontier 能不能被展开，如果不能被展开，就代表没有解，则返回失败。如果 frontier 有解的话，我们就从 frontier 里面拿出一个叶节点，然后判断一下拿出来的节点是不是目标，如果是的话，我们就可以返回解决方案了。

如果不是目标的话，那我们还要继续展开这个叶节点，然后把新获得的节点加到 frontier 开节点集合里面。提供给下一次循环来选择展开用。

这些叶节点都是开节点，因为它们都没有被展开过。

那么不断循环，这就是树搜索。我们最开始有一个根节点，开展以后把叶节点都放到 frontier 集合里面，然后取出一个来再展开，然后新获得的节点再放到 frontier 集合里面。

这个树搜索，并没记住我们以前展开过什么的，只是在不停地展开。

图搜索：

我们看看 Graph-Search 这个函数。它的输入输出和树搜索是一样的。输入。。。输出。。。

那么这里黑体字是新加的一些操作。

Initialize the explored set to be empty，我们初始化一个空的闭节点集合，定义这个新变量的目的是用来存储哪些节点已经被展开搜索过的。然后开始循环，这跟刚才树搜索是一样的。Frontier 如果为空，则返回 failure。如果有也叶节点，则选择一个叶节点，如果叶节点是目标，则找到解了。否则的话，add the node to the explored set，把这个节点放到闭节点集合里面，代表这个节点已经被探索展开过了。后面就是把它的儿子都加到 frontier 集里面。但这里有个条件，only if not in the frontier or explored set，这个地方我做了一个重复判断，就是如果加这个新节点的时候，我们要看看这个节点在不在 frontier 里面，以及在不在已经被搜索过的节点集合里面，如果在的话就不加了。只有它不在的时候，我们才做这个事情。那么这个就是图搜索和树搜索的不同。

图搜索用 explored set 这个机制，就可以避免重复地搜索某些节点。

搜索算法的评价

• 完备性 Completeness: 如果存在解，该算法是否一定会找到解?
• 最优性 Optimality: 该算法是否能够找到最优解?
• 时间复杂度 Time complexity: 算法找到解需要花长时间?
• 空间复杂度 Space complexity: 算法需要多少内存用于搜索?

问题难度和算法复杂度

• 问题的难度 problem difficulty 两种方法来度量：图规模和搜索树规模：
  • 图规模（对应图搜索）
    • 当输入是一个图时，例如罗马尼亚地图寻径问题，理论上，我们用状态空间图的大小来衡量问题的规模 |V | + |E|, V 是点数 ，E 边数。
  • 搜索树的规模（对应树搜索）
    • 用如下二个指标来度量:
      • b, 分支数 branching factor 或者节点所具有的最大子节点数目；
      • d, depth，最浅的目标状态所在；
• 算法复杂度
  • 时间复杂度经常用搜索树展开的节点的数目表示。
  • 空间复杂度通常用需要存储的最大节点数目来估计。

无信息搜索

无信息搜索是指在搜索过程中不使用任何启发信息的搜索方法。无信息搜索方法通常会遍历整个搜索空间，直到找到解或者确定无解。

无信息搜索可以理解为，没有任何的先验知识，就是盲目地去试（尽管盲目地试的时候也可以有些尝试时优先级策略）。

搜索算法的一般存储框架

BFS

DFS

有信息搜索